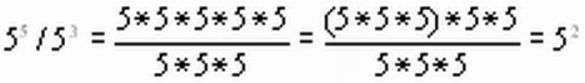
Możemy zatem zapisać :
n = sin ( z )
Ale z formalnego punktu widzenia równie dobrze moglibyśmy zapisać :
z = sin ( n )
Ale by móc zweryfikować poprawność powyższego zapisu, powinniśmy mieć możliwość odtworzenia w jakiś sposób nieznanej dotychczas wartości liczby n . Do rekonstrukcji tej nieznanej wartości służy funkcja odwrotna do funkcji sinus , czyli funkcja arcus sinus ; zresztą pozostałe funkcje trygonometryczne również dysponują funkcjami odwrotnymi do nich :
| Funkcje trygonometryczne | Funkcje odwrotne do nich |
|---|---|
| cos | arcus cosinus |
| tangens | arcus tangens |
| cotangens | arcus cotangens |
( Funkcje odwrotne do funkcji trygonometrycznych noszą nazwę funkcji cyklometrycznych . )
Zapomnijmy na jakiś czas o funkcjach trygonometrycznych i cyklometrycznych i zajmijmy się funkcją wykładniczą, czyli funkcją o postaci :y = a x
Stosując poprzednio zaproponowaną konwencję dotyczącą wielkość znanych i nieznanych możemy funkcję wykładniczą zapisać następująco :
n = a z
Ale z formalnego punktu widzenia mielibyśmy w pełni prawo zastąpić miejscami wielkości : znaną i nieznaną :
z = a n
W takim przypadku może zajść potrzeba odtworzenia wartości zmiennej n , czyli przydałaby się odpowiednia funkcja odwrotna. Funkcja odwrotna do funkcji wykładnicznej to funkcja o nazwie logarytm i zapisuje się ją następująco :n = log a ( z )
( Jeżeli liczba a , zwana podstawą potęgi lub podstawą logarytmu , jest równa 10, to wówczas omija się ją przy zapisie logarytmu. )
Ponieważ najbardziej charakterystyczne właściwości funkcji logarytm wynikają z właściwości funkcji wykładniczej , zatem skupmy wstępnie uwagę na własnościach tejże funkcji, a zwłaszcza na jednej z nich :
y = a x ∗ a z = a ( x + z )
Analogicznie można zapisać :
y = a x ⁄ a z = a ( x - z )
Własność iloczynu dwóch funkcji wykładniczych ( który jest równy funkcji wykładniczej o tej samej podstawie, ale o wykładniku sumacyjnym ) można wykazać w sposób "quasi - empiryczny" :
5 3 ∗ 5 2 = ( 5 * 5 * 5 ) * ( 5 * 5 ) = 5 * 5 * 5 * 5 * 5 = 5 5
( Wystarczy podsumować liczbę mnożonych przez siebie "piątek", już po usunięcie nawiasów, aby uzyskać wartość wykładnika wypadkowego - "sumacyjnego". )
W podobny, "empiryczny" sposób możemy udowodnić drugi ze wzorów - tzw. wzór "ilorazowo - różnicowy" :
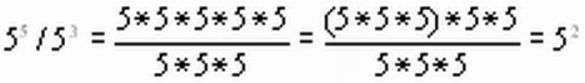
( Aby uzyskać iloczyn dwóch "piątek" wystarczy iloczyn zawarty wewnątrz pary nawiasów "uprościć" z mianownikiem. )
Zanim przejdziemy od własności funkcji wykładniczych do własności logarytmów zwróćmy uwagę na fakt, że operacja złożenia pewnej funkcji "pierwotnej" z jej funkcją odwrotną da w efekcie argument "najbardziej wewnętrzny" owej funkcji złożonej ; dla przykładu złożenie funkcji trygonometrycznej i odpowiedniej arcus funkcji da w efekcie argument funkcji "bardziej wewnętrznej" :arcsin [ sin ( x ) ] = sin ( arcsin ( x ) ] = x
Odnieśmy tę samą prawidłowość do złożenia ( superpozycji ) funkcji wykładniczej i logarytmu :
a log a ( x ) = x
Wykorzystamy tę tożsamość do konstrukcji wyrażenia opisującego logarytm iloczynu ( dwóch wielkości ) :
log a ( b * c ) = log a ( a log a ( b ) * a log a ( c ) ) = log a ( a [ log a (b ) + log a ( c ) ] ) = log a ( a w )
( gdzie w ( "wykładnik" ) jest sumą obu logarytmów : logarytmu z b oraz logarytmu z c ).
Na mocy definicji logarytmu otrzymamy :
log a ( b ∗ c ) = log a ( a w ) = w = log a ( b ) + log a ( c )
Na mocy tak wyprowadzonego wzoru możemy wyprowadzić następny wzór opisujący logarytm potęgi ; wystarczy przyjąć, że : b = c ; otrzymamy zatem :log a ( b 2 ) = log a ( b ∗ b ) = log a ( b ) + log a ( b ) = 2 ∗ log a ( b )
Uzyskane rozwiązanie możemy uogólnić na potęgi wyższych stopni :
log a ( b 3 ) = log a ( b 2 * b ) = 2 ∗ log a ( b ) + log a ( b ) = 3 ∗ log a ( b )
Wzory "podwójne" są następujące :
cos ( 2 α ) = 2 cos 2 ( α ) - 1
sin ( 2 α ) = 2 sin ( α ) cos ( α )
( Inne postacie wzoru na cosinus kąta podwojonego wynikają ze zastosowania wzoru jedynkowego . )
Wzory te można sprawdzić na następującej stronie internetowej :
http://www.matma.net.pl/trygon.php
W pierwszej kolejności postaramy się wyprowadzić wzór na cosinus kąta podwojonego korzystając z twierdzenia cosinusów zwanego też twierdzeniem Carnota .Zastosujmy to twierdzenie dwukrotnie w przypadku pewnego trójkąta równoramiennego :
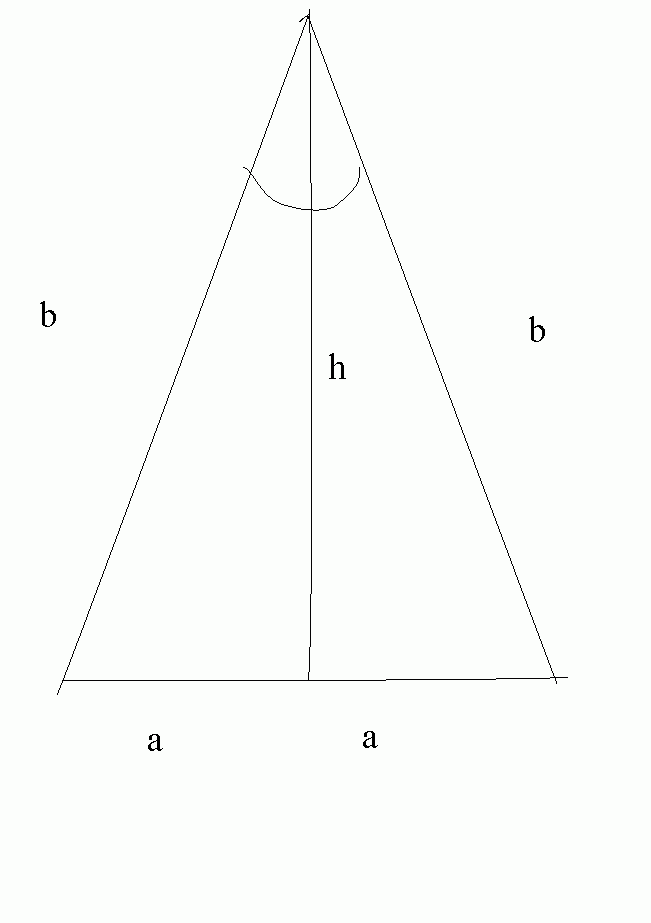
h = b ∗ cos α
Zastosujmy teraz wzór Carnota do dwóch trójkątów :
Oto zapisy obu tych zastosowań wzoru Carnota :
W drugim z tych równań wstawiamy wyznaczoną wcześniej postać h uzyskując :
a 2 = b 2 ∗ ( 1 - cos 2 α )
Rozwiązując ( a raczej - przekształcając ) ten układ równań uzyskujemy ostatecznie :
cos 2 α = 2 cos 2 α - 1
Korzystamy teraz z przekształconego wzoru jedynkowego odniesionego do kątów połowkowych :
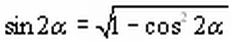
Cosinus kąta podwojonego wyrazimy korzystając z alternatywnego wzoru :
cos 2 α = cos 2 α - sin 2 α
Wyrażenie to podstawimy pod znak pierwiastka ; pod znak pierwiastka podstawimy również zamiast jedynki bardziej skompliowane wyrażenie korzystając ze zależności :1 = 1 2 = sin 2 + cos 2 = ( sin 2 + cos 2 ) 2
Podstawiając jednocześnie oba te wyrażenia pod znak pierwiastka otrzymamy ostatecznie :
sin 2 α = √ ( 4 ∗ sin 2 α ∗ cos 2 α ) = 2 sin ( α ) cos ( α )
( Wzory "podwojone" mogą się przydać np. przy analizie częstotliwości migotania światła emitowanego przez świetlówkę lub miniaturową żaróweczkę zasilaną prądem zmiennym )